快速入门

欢迎来到 SU2 套装的快速快速入门教程。本教程的初衷是通过一个易于获取的格式来说明分析和设计工具的一些主要特点。仅需较短时间即可完成该教程。如若您还未准备完全，请进入下载页（Download）获取最新稳定的发行版软件和安装页（Installation）获取安装教程。该教程仅使用与 SU2 套装的 SU2_CFD 工具。

1. 目标

完成该教程后，用户将熟悉二维几何中的无粘外部流动的流动和连续伴随模拟（continuous adjoint simulation ），并且能够绘制流动解和由结果表面灵敏度（sensitivities）的图像。教程所选择的几何模型为 NACA 0012 翼型。因此，教程将展示 SU2 的一下能力：

• 二维稳态欧拉和连续伴随欧拉方程；
• 多重网格；
• 空间离散中 JST 数值格式；
• 欧拉隐式时间积分；
• 欧拉壁面和远场边界条件。

2.源

SU2/QuickStart/directory （SU2/QuickStart/）文件夹下包含运行本教程所需的文件。对于其他教程，TestCases/ repository 文件夹中提供了所需文件。代码所需两个文件作为输入文件：描述特定问题选项的配置问题（configuration file）及其所对应的计算网格文件（mesh file）。用户可在 QuickStart/ 文件夹中或TestCases/euler/naca0012 下的TestCases 仓库找到上述文件。

3.教程

下面的教程将引导您完成使用 SU2 计算 NACA 0012 机翼周围的(空气)流动和邻接解所需的步骤。至此，假定用户已经获得并编译了 SU2_CFD 代码（单独或作为完整 SU2 软件包的一部分）以进行串行计算。如果您尚未完成这一要求，请参阅下载和安装页面。

背景

NACA 0012 翼面是美国国家航空咨询委员会（National Advisory Committee for Aeronautics, NACA）开发的四位数翼面之一，是众多 CFD 测试案例中广泛使用的几何形状。其编号系统如下：第一个数字表示最大外倾（以弦的百分比为单位），第二个数字表示最大外倾的位置（以弦的百分之几十为单位），最后两位数字表示最大厚度（以弦的百分比为单位）。有关这些翼面截面的更多信息，请参见此处或 Abbott 和 von Doenhoff 合著的《Theory of Wing Sections》一书。

问题设置

本算例将求解攻角为 1.25 度时 NACA 0012 机翼上的欧拉方程，自由流条件如下：

• 压力 = 101325 Pa
• 温度 = 273.15 K
• 马赫数 = 0.8

目的是找到与目标函数（定义为机翼上的阻力）相关的流动解和邻接解。

网格描述

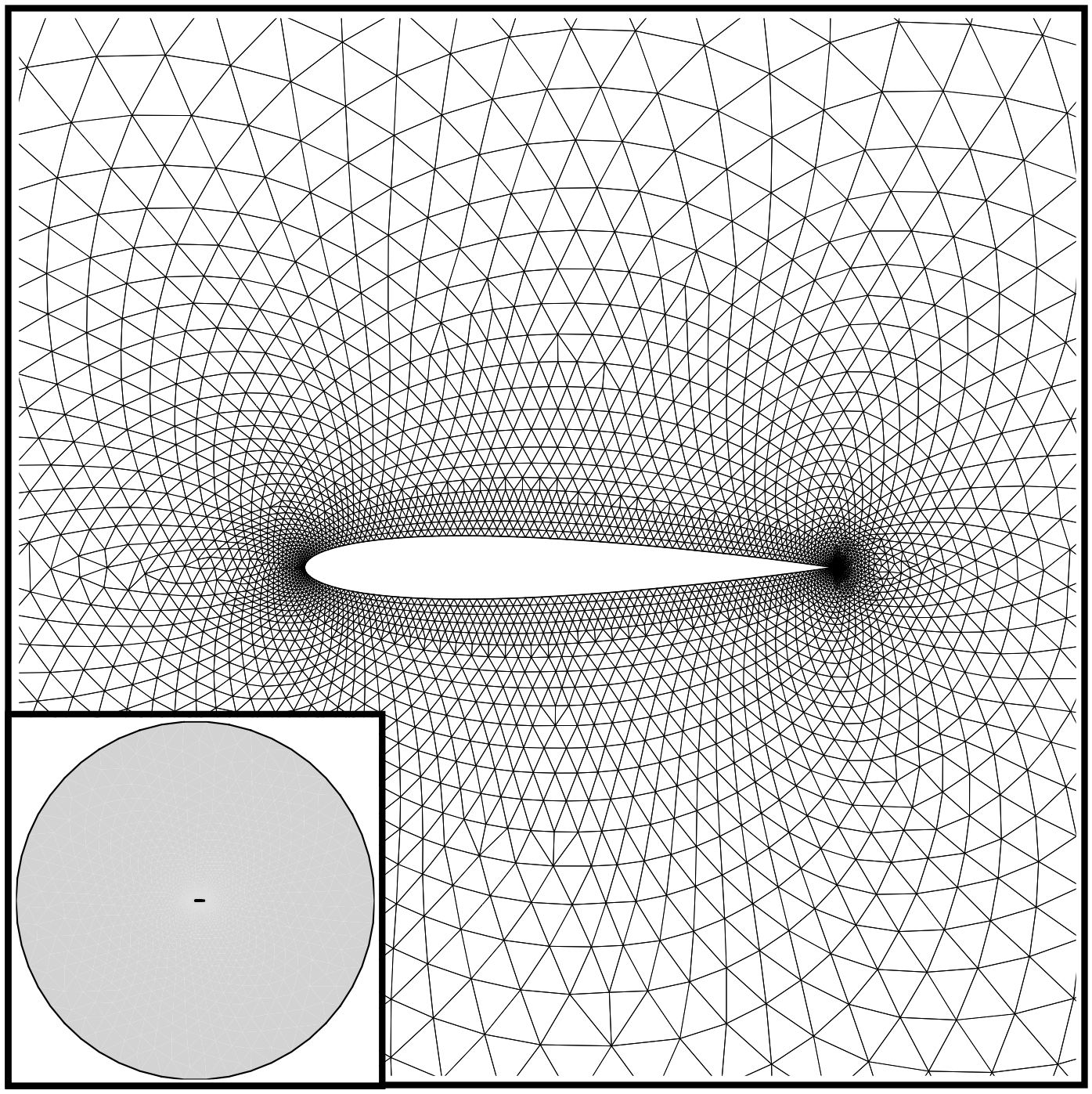
（本算例）所提供的非结构网格为自带的 .su2 格式。它由 10216 个三角形单元、5233 个点和两个名为翼面和远场的边界（或 “marker”）组成。翼面使用流动切线欧拉壁边界条件，而远场使用标准的基于特性（值）的边界条件，下图为网格视图。

应用直接法求解问题相关的配置文件

除网格外，运行 SU2_CFD 求解器所需的唯一文件就是详细的配置选项。它定义了问题，包括数值方法、流动条件、多重网格等所有选项，还指定了输入网格和输出文件的名称。为保持本教程的简洁性，将只讨论两个配置选项。其余教程将讨论更多配置选项。

在文本编辑器中打开 inv_NACA0012.cfg 文件后，其中一个早期选项是 MATH_PROBLEM：

% Mathematical problem (DIRECT, CONTINUOUS_ADJOINT)
MATH_PROBLEM= DIRECT

SU2 能够运行多组方程的直接问题和伴随问题。直接分析可求解几何体周围的流动，并计算出相关量，如体上的升力和阻力系数。通过求解伴随问题，可以采用一种有效的方法，获得单一目标函数（如阻力系数）相对于大量设计变量（表面变形）的变化。在进行空气动力学形状设计时，直接求解和邻接求解通常可以提供优化器所需的目标分析和梯度信息。在本教程中，首先对 NACA 0012 机翼进行直接模拟。

用户还可以设置输出文件的格式：

 % Output file format<br> OUTPUT_FILES= (RESTART, PARAVIEW, SURFACE_CSV)

SU2 支持输出 .vtu （ParaView）、.dat （Tecplot ASCII）和 .szplt （Tecplot 二进制）格式的解决方案文件，这些文件可分别在 ParaView 和 Tecplot 可视化软件包中打开。在本教程中，我们将文件类型设置为 PARAVIEW：为了使求解所得的物理场可视化，鼓励用户下载并使用免费的 ParaView 软件包。机翼边界数据的输出格式设置为 SURFACE_CSV（逗号分隔值）：生成的文本文件可使用各种图形工具或 LaTeX 软件包（如 PGFPlots）绘制。注意，如果配置文件中没有 OUTPUT\_FILES 选项，其默认值为（RESTART, PARAVIEW, SURFACE\_PARAVIEW）。

运行 SU2 直接法进行分析

本教程的第一步是求解欧拉方程：

1. 跳转至至 QuickStart/ 目录或者创建一个运行本教程的目录。如果创建了新目录，请将配置文件 (inv_NACA0012.cfg) 和网格文件 (mesh_NACA0012_inv.su2) 复制到该目录。
2. 在命令行输入SU2_CFD inv_NACA0012.cfg 运行可执行文件。如果未正确设置环境变量，则需要在命令行中指定 SU2_CFD 可执行文件的路径。
3. 每次迭代后，SU2 将在流动求解器更新并打印打印残差，当残差将在达到指定的收敛标准后，程序停止计算。
4. 退出 SU2 后，将写入包含流动结果（文件名中包含 “flow”）的文件。可通过 ParaView (.vtu) 或 Tecplot (.dat 或 .szplt) 查看求解结果。文件如下：

• flow.vtu（或 flow.szplt）-> 整个体积的流动求解结果
• surface_flow.csv（或 surface_flow.vtu（或 surface_flow.szplt））-> 包含机翼表面数值的文件。
• restart_flow.dat -> 内部格式的重启文件，用于在 SU2 中重启该模拟。
• history.csv（或 history.dat）-> 包含收敛历史信息的文件。

直接法的结果分析

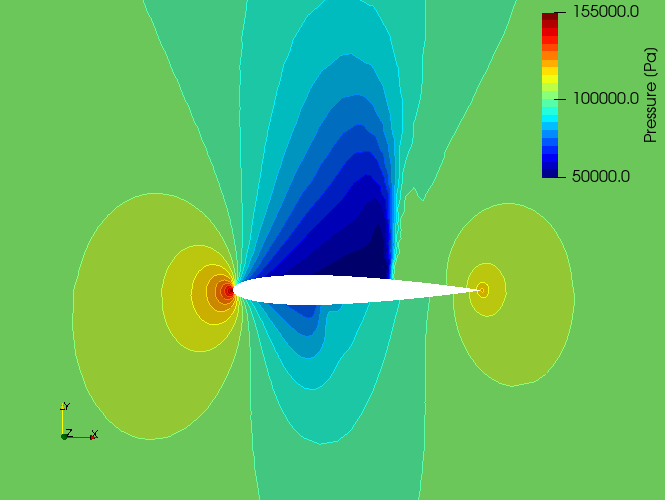
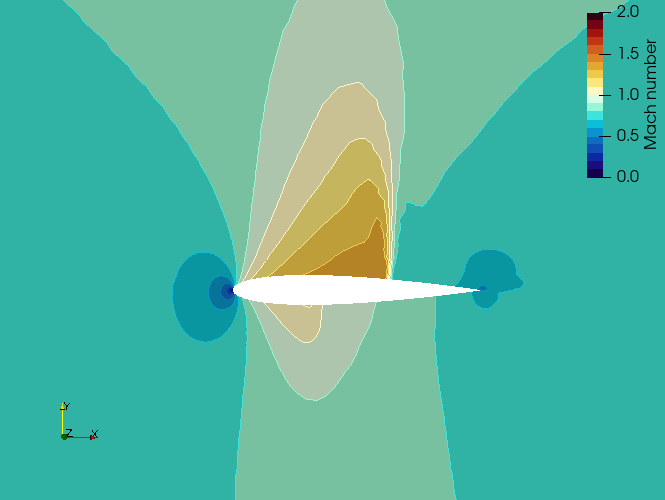
使用 SU2（求解） 结果在 ParaView 中创建的（云图）如下所示。求解结果包含在 flow.vtu 文件中。

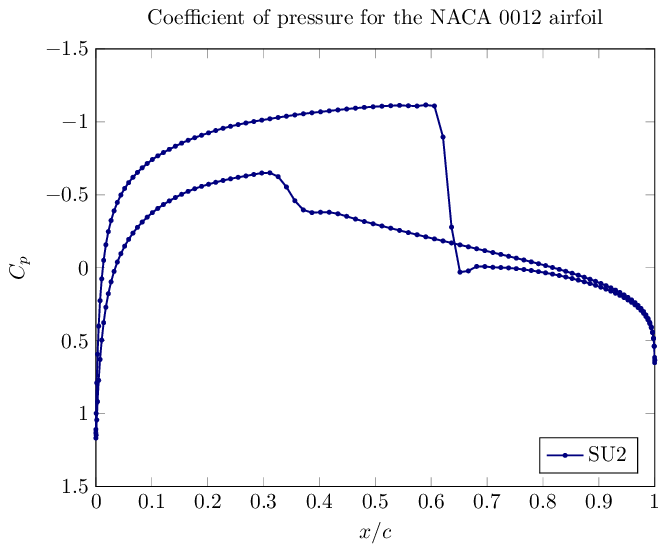
下图是将 SU2 （求解）结果导入含有 PGFPlots 的 LaTeX 中绘制的 (压力分布系数）图。（求解）结果包含在 surface_flow.csv 文件中。

运行 SU2 伴随法进行分析

接下来运行伴随法进行求解，进而获得目标函数（机翼上的阻力）对来流条件的敏感性：

1. 打开配置文件，将参数 MATH\_PROBLEM 由 DIRECT 改为 CONTINUOUS_ADJOINT，将参数 OUTPUT_FILES 由 (RESTART、PARAVIEW、SURFACE_CSV) 改为 (RESTART、SURFACE_CSV)；保存该文件。
2. 将重启文件（restart_flow.dat）重命名（或同名链接）为 “solution_flow.dat”，以便伴随法代码可以获取直接法的解。
3. 在命令行输入 SU2_CFD inv_NACA0012.cfg，再次运行可执行文件。
4. SU2 将在每次迭代时打印残差更新，并在达到指定的收敛标准后结束计算。
5. 退出 SU2 后，将写入包含伴随结果（文件名中包含 “adjoint”）的文件。具体地说，这些文件是：

• surface_adjoint.csv（或 surface_adjoint.vtu、surface_adjoint.szplt）-> 包含沿翼面的伴随值的文件。
• restart_adj_cd.dat -> 内部格式的重启文件，用于在 SU2 中重启该模拟。注意，目标名称会出现在文件名中。
• history.csv（或 history.dat）-> 包含收敛历史信息的文件。
• (adjoint.vtu 或 adjoint.szplt（如有需要）- 全体积伴随解，可在 ParaView 或 Tecplot 中显示。

注意，从 SU2 v4.1 或更高版本开始，用户也可以计算欧拉方程的离散邻接。如果您已构建了支持算法微分的代码，则可以通过以下步骤运行离散矢量：

1. 打开配置文件，将参数 MATH_PROBLEM 更改为 DISCRETE_ADJOINT，将参数OUTPUT_FILES 更改为 (RESTART, SURFACE_CSV)；保存此文件。
2. 将重启文件（restart_flow.dat）重命名（或同名链接）为 “solution_flow.dat”，以便伴随法代码可以访问直接法的解。
3. 在命令行输入 SU2_CFD_AD inv_NACA0012.cfg 运行可执行文件。注意，SU2_CFD_AD 可执行文件只有在编译了支持 AD 的源代码后方可用。
4. SU2 将在每次迭代邻接求解器时再次打印残差更新，仿真将在达到指定收敛标准后结束。
5. 在退出 SU2 时，将写入包含邻接结果的类似文件。

SU2 伴随法结果分析

下图是将 SU2 （求解）结果导入含有 PGFPlots 的 LaTeX 中绘制的 (NACA 0012 机翼表面敏感度分布）图，并比较了连续和离散伴随法的求解结果。这些结果包含在两个 surface_adjoint.csv 文件中。

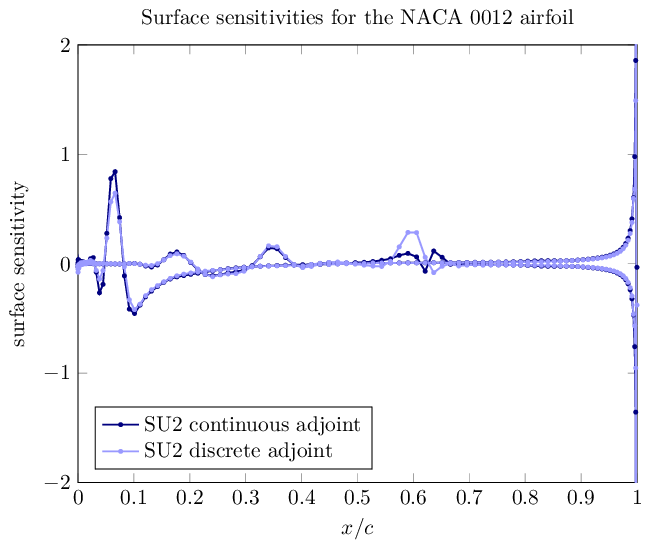
这些值可以通过本教程未说明的附加步骤，在机翼表面的每个节点上根据流动和邻接解进行细化，计算成本可忽略不计。

结论

恭喜您！您已经成功地使用 SU2 进行了第一次流动模拟。请继续阅读本教程教程，从而获得更多（如何）使用代码的信息，也不要忘记阅读用户指南中的信息。在快速入门或结果可视化方面遇到问题？请访问FAQs问题页面或 CFD-online 论坛。

原文链接：Quick Start (su2code.github.io)

Views: 52